Калашников Сергей Григорьевич . Электричество: Учебн. пособие. — 6-е издание, ФИЗМАТЛИТ, 2003 г.
Книга написана на основе курса лекций, прочитанных автором в течение многих лет на физическом факультете Московского государственного уни- верситета.
Альтернативные источники информации по материалу: Закон Кулона.

Электрические заряды

Закон взаимодействия электрических зарядов. § 2

Начало количественного изучения электрических явлений относится к концу XVIII века, когда Кулон (1985 г.) установил на опыте закон взаимодействия электрических зарядов.

Для заряженных тел произвольных размеров такой закон в общей форме дать нельзя, так как сила взаимодействия тел зависит от их формы и взаимного расположения.

Однако форма тел и их взаимная ориентировка перестают сказываться, если размеры тел весьма малы по сравнению с расстоянием между ними. Поэтому закон взаимодействия, имеющий общее значение, можно установить только для точечных зарядов. Так как электрические заряды всегда распределены в объеме, то никаких конечных зарядов в математической точке, разумеется, быть не может. Под точечным зарядом в физике всегда понимают протяженное заряженное тело, размеры которого весьма малы по сравнению с расстоянием отдругих зарядов. 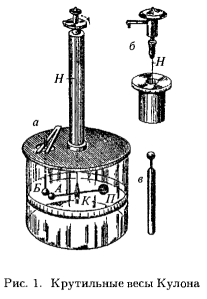Схема опытов Кулона изображена на рис. 1 (а — общий вид прибора, б — его головка, в — проводник для зарядки шариков А и Б). На тонкой металлической нити Н подвешено легкое изолирующее коромысло К, имеющее на одном из концов шарик А, а на другом — противовес П. Верхний конец нити закреплен на вращающейся головке прибора, позволяющей точно отсчитывать угол закручивания нити. Внутрь прибора можно вносить второй изолированный шарик Б такого же размера, какшарик А. Большой стеклянный цилиндр защищает чувствительные части прибора от движения воздуха.

Чтобы установить, как зависит сила взаимодействия от расстояния между зарядами, шарикам А и Б сообщают произвольные заряды, касаясь их третьим заряженным шариком, укрепленным на изолирующей ручке. Шарики отталкиваются и устанавливаются на некотором расстоянии, которое измеряют, пользуясь шкалой прибора. Затем вращают головку прибора и закручивают нить подвеса, замечая при этом расстояния, до которых сближаются шарики при различных углах закручивания нити. Как известно из механики, при деформации кручения (в области обратимых упругих деформаций) угол закручивания пропорционален моменту крутящей силы; зная, во сколько раз мы увеличили угол закручивания нити, мы тем самым определяем, во сколько раз увеличился момент силы, а отсюда можно определить и силу, действующую на шарик коромысла. В результате этих опытов Кулон заключил, что сила взаимодействия двух точечных зарядов направлена вдоль линии, соединяющей оба заряда, и обратно пропорци- ональна квадрату расстояния между зарядами:

F = 1/r².

Сила взаимодействия между шариками зависит еще от зарядов шариков. Эту зависимость можно выяснить при помощи следующего опыта. Если коснуться на короткое время одного из шариков, А или Б, другим шариком, имеющим такие же размеры, но не заряженным, то в силу тождественности обоих соприкасающихся шариков заряд распределяется между ними поровну. При этом оказывается, что сила взаимодействия между шариками А и Б, на одном из которых теперь находится лишь половина первоначального заряда, при том же расстоянии уменьшается в два раза. Повторяя этот прием, можно уменьшить заряд шарика в два, четыре и т.д. раз и убедиться, что сила взаимодействия пропорциональна заряду каждого из шариков.

Более точно этот вопрос можно исследовать следующим образом. Сообщим шарикам А и В некоторые (неизвестные) заряды и измерим силу взаимодействия Fab между ними при некотором определенном расстоянии. Заменим, далее, шарик Б другим заряженным шариком В и измерим снова силу взаимодействия Fab между А и В при том же расстоянии, что и в первом случае. Если теперь изменить произвольным образом заряд шарика А и опять измерить силы взаимодействия шарика А с шариками Б и В, то опыт показывает, что отношение сил Fab /Faв в обоих случаях одинаково, т.е. не зависит от заряда шарика А. Это значит, что указанное отношение сил зависит только от зарядов шариков Б и В, а следовательно, можно положить его равным отношению зарядов обоих шариков, т.е.

Fab/Faв = qб/qв

Это соотношение является определением отношения двух зарядов и указывает способ сравнения зарядов.

Полученный результат показывает, что сила взаимодействия пропорциональна заряду одного из шариков (А). Так как оба шарика в этих опытах равноправны, то отсюда следует, что сила взаимодействия пропорциональна каждому из зарядов q1 и q2

Таким образом, сила взаимодействия двух точечных зарядов равна:

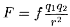
Здесь f — коэффициент пропорциональности, зависящий от выбора единиц заряда, расстояния и силы.

Для того чтобы выразить не только модуль силы, но и ее направление, закон Кулона можно представить в векторной форме:

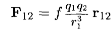
где F12 — вектор силы, действующей на заряд 2 со стороны заряда 1, а r12 — радиус-вектор, направленный от заряда 1 к заряду 2.

Опыты Кулона, конечно, не являются единственным доказательством справедливости закона обратных квадратов. В настоящее время имеется большое количество других экспериментальных данных, показывающих, что закон Кулона выполняется очень точно и притом как для очень больших, так и для очень малых расстояний. В частности, исследования атомных явлений позволяют заключить, что он справедлив, по крайней мере, вплоть до расстояний порядка 10^-15 м.

Абсолютная электростатическая система единиц. § 3

Для определения коэффициента пропорциональности f в законе Кулона мы должны остановиться на какой-либо определенной системе единиц.

Всякая система единиц состоит из некоторого числа основных единиц, выбираемых независимо друг от друга, и совокупности производных единиц. Последние образуются из основных (и других производных) единиц с помощью подходящим образом выбранных соотношений, выражающих определенные физические законы и связывающих между собой данную физическую величину, для которой устанавливается единица, с другими величинами, единицы которых уже определены. Каждое такое соотношение, используемое для установления той или иной производной единицы, мы будем называть определяющим соотношением для данной единицы.

В физике до настоящего времени часто употребляют абсолютную систему единиц (механических, электрических и магнитных) СГС, построенную на трех основных единицах: длины (сантиметр), массы (грамм) и времени (секунда). Единицей силы в этой системе служит дина. Если выражать расстояние r в сантиметрах, а силу F в динах, то в законе Кулона будет единственная неопределенная единица — единица заряда. Поэтому можно выбрать эту единицу таким образом, чтобы было f = 1, т.е. чтобы закон Кулона приобрел наиболее простую форму. Такая единица заряда получила название абсолютной электростатической единицы заряда.

Полагая в формуле r = 1, q1 = q2 = 1, получаем F = 1. Это значит, что абсолютная электростатическая единица заряда есть такой заряд, который действует в вакууме на равный ему заряд, удаленный на расстояние 1 см, с силой 1 дин.

Если выражать заряды в абсолютных электростатических единицах, силу — в динах, а расстояние — в сантиметрах, то закон Кулона принимает вид:

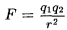
Выбирая за основные единицы сантиметр, грамм и секунду и пользуясь абсолютной электростатической единицей заряда, можно определить единицы всех электрических и магнитных величин, с которыми мы познакомимся в дальнейшем. Такая система единиц называется абсолютной электростатической системой и обозначается символом СГСЭ.

Таким образом, в системе СГСЭ единица заряда есть производная единица. Определяющим соотношением для нее служит закон Кулона.

Введение >> Закон Кулона >> Продолжение следует.